What is differential privacy?
|
Differential privacy has emerged as the gold standard for privacy preserving statistical analysis. If you’re doing an analysis of a population, and you want to share statistics about it without compromising the privacy of individuals in the dataset, differential privacy is the very best way to do it.
The video to the right is a quick explainer that many find helpful to understand the primary concepts at play in differential privacy. |
|
Here is an intentionally simplified explanation of the Differential Privacy Mechanism, and how it works to enable valuable information without sacrificing privacy of individuals.
Your friends and family know that you have an allergy to nuts. But this is not public information you want everyone to know. Being able to keep a secrets is called privacy.
If you go out to eat with a group, the person making dinner needs to know if someone in the group has a nut allergy. But the chef doesn’t necessarily need to know who is the one who can't have their famous peanut sauce. They just need to know that of the people at dinner, someone can't have nuts.
Now imagine the person or people with the nut allergy leaves the table. For dessert, the table lets the waiter know that pad Thai is now ok to serve. Oops! Now the waiter knows exactly who was allergic. So much for privacy.
Differential privacy works to protect against these kinds of scenarios by adding noise to statistics in order to blur the contribution of individuals, while preserving the information about the group.
In the example above, this means that some known percentage of the time, the chef receives reports of nut allergies when in reality it was just made up by the server. So the chef is never sure if it's a real allergy being reported, or just a practical joke (aka random noise).
Imagine it like pixelating an image of bridge – as noise is added, you can still tell the image is a bridge, and even that its a suspension bridge, but you can no longer identify which specific bridge it is.
Your friends and family know that you have an allergy to nuts. But this is not public information you want everyone to know. Being able to keep a secrets is called privacy.
If you go out to eat with a group, the person making dinner needs to know if someone in the group has a nut allergy. But the chef doesn’t necessarily need to know who is the one who can't have their famous peanut sauce. They just need to know that of the people at dinner, someone can't have nuts.
Now imagine the person or people with the nut allergy leaves the table. For dessert, the table lets the waiter know that pad Thai is now ok to serve. Oops! Now the waiter knows exactly who was allergic. So much for privacy.
Differential privacy works to protect against these kinds of scenarios by adding noise to statistics in order to blur the contribution of individuals, while preserving the information about the group.
In the example above, this means that some known percentage of the time, the chef receives reports of nut allergies when in reality it was just made up by the server. So the chef is never sure if it's a real allergy being reported, or just a practical joke (aka random noise).
Imagine it like pixelating an image of bridge – as noise is added, you can still tell the image is a bridge, and even that its a suspension bridge, but you can no longer identify which specific bridge it is.
The amount of noise added is a trade-off – adding more noise makes the data more anonymous, but it also makes it less useful. This parameter enables tradeoffs of risk depending on the use case.
For example, Google sharing individuals’ location data is about as sensitive as it comes, but a carbon derivative or savings from an efficiency project is already abstracted and carries much less risk. With differntial privacy, the amount of noise can be adjusted and privacy set based on the use case.
In their paper, Differential Privacy for Social Science Inference, D'Orazio, Honaker and King explain differential privacy further, and how to realize differential privacy in a variety of common tasks for analysis. This is a paper worth reading closely for a deeper dive, especially the first half.:
For example, Google sharing individuals’ location data is about as sensitive as it comes, but a carbon derivative or savings from an efficiency project is already abstracted and carries much less risk. With differntial privacy, the amount of noise can be adjusted and privacy set based on the use case.
In their paper, Differential Privacy for Social Science Inference, D'Orazio, Honaker and King explain differential privacy further, and how to realize differential privacy in a variety of common tasks for analysis. This is a paper worth reading closely for a deeper dive, especially the first half.:
|
Social scientists often want to analyze data that contains sensitive personal information that must remain private. However, common techniques for data sharing that attempt to preserve privacy either bring great privacy risks or great loss of information. A long literature has shown that anonymization techniques for data releases are generally open to reidentification attacks. Aggregated information can reduce but not prevent this risk, while also reducing the utility of the data to researchers. Even publishing statistical estimates without releasing the data cannot guarantee that no sensitive personal information has been leaked. Differential Privacy, deriving from roots in cryptography, is one formal, mathematical conception of privacy preservation. It brings provable guarantees that any reported result does not reveal information about any one single individual.
|
Can’t we just aggregate data and remove identifiers?
It turns out that intuitive approaches for anonymization just don’t work. A large body of research since the 60s has demonstrated that existing approaches to anonymization such as aggregation, identifier removal, and k-anonymity have significant weaknesses. Even worse, these weaknesses are growing easier to exploit as more and varied data are collected about individuals -- and when it comes to smart meter data and buildings, there is a lot of varied data available.
As privacy practitioners say, “Your anonymous data isn’t.”
The US Census, which found that its statistics were extremely vulnerable to reconstruction attacks, provides one of many timely examples of this problem. The 2020 decennial census will use differential privacy as a result.
As privacy practitioners say, “Your anonymous data isn’t.”
The US Census, which found that its statistics were extremely vulnerable to reconstruction attacks, provides one of many timely examples of this problem. The 2020 decennial census will use differential privacy as a result.
|
The US Census, which found that its statistics were extremely vulnerable to reconstruction attacks, provides one of many timely examples of this problem. The 2020 decennial census will use differential privacy as a result.
|
|
|
Dr. Cynthia Dwork, the inventor of differential privacy, presents a number of eye-popping examples of the weaknesses of traditional approaches in her Turing Lecture:
Turing Lecture: Dr Cynthia Dwork, Privacy-Preserving Data Analysis |
|
Haven't Regulators Already Given Us 15/15 Aggregation? Isn't that Enough?
See application of EDP in our GRIDmeter work here.
The California Public Utility Commission Decision 14-05-016 defines a limited procedure for anonymizing energy data. It is restricted to monthly average consumption by zip code. If at least 15 meters are aggregated together and no single meter comprises more than 15% of the total energy consumption, then the data are considered “anonymous”.
The trouble is that this procedure is not defined for AMI interval data (minutely, hourly, daily, etc.). Further, it is not defined for aggregation by criteria other than zip code. In conversations with regulators, we found the law is ambiguous: not explicitly denying other types of aggregations, but not defining exactly what is good enough.
For Recurve, differential privacy is valuable for when we would like to share statistical outputs with stakeholders that do not have permission to access customer data.
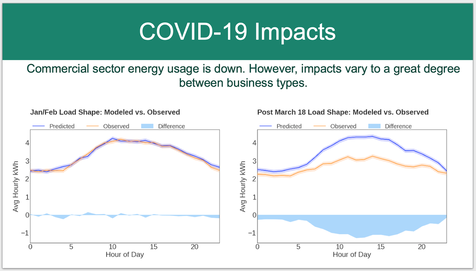
A recent example was our work with COVID-19 analytics. We used MCE’s data but wanted to share the outputs outside of MCE. We prepared differentially private versions of the statistics, which were shared with a wide variety of stakeholders (and publicly in the meeting notes) at the California Energy Efficiency Coordinating Committee (CAEECC).
The trouble is that this procedure is not defined for AMI interval data (minutely, hourly, daily, etc.). Further, it is not defined for aggregation by criteria other than zip code. In conversations with regulators, we found the law is ambiguous: not explicitly denying other types of aggregations, but not defining exactly what is good enough.
For Recurve, differential privacy is valuable for when we would like to share statistical outputs with stakeholders that do not have permission to access customer data.
A recent example was our work with COVID-19 analytics. We used MCE’s data but wanted to share the outputs outside of MCE. We prepared differentially private versions of the statistics, which were shared with a wide variety of stakeholders (and publicly in the meeting notes) at the California Energy Efficiency Coordinating Committee (CAEECC).
